Let us start with numbers
 |
(1)
|
where 
, 
, 
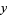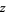, and 
are integers, has no nonzero solutions for 
has come to be known as Fermat's Last Theorem. It was called a "theorem" on the strength of Fermat's statement, despite the fact that no other mathematician was able to prove it for hundreds of years.
, , , and 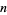are integers, has no nonzero solutions for 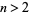has come to be known as Fermat's Last Theorem. It was called a "theorem" on the strength of Fermat's statement, despite the fact that no other mathematician was able to prove it for hundreds of years.
Let us read this in Latin
"Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet" (Nagell 1951, p. 252). In translation, "It is impossible for a cube to be the sum of two cubes, a fourth power to be the sum of two fourth powers, or in general for any number that is a power greater than the second to be the sum of two like powers. I have discovered a truly marvelous demonstration of this proposition that this margin is too narrow to contain."
so what is the big deal?
One of the Ted Talk I watched toady talked about teaching kids statistics and Probability. The Drunkard walk is a book that should be mandatory reading for every one.!!!
Think about this problem - if there are 11 people soccer players and 2 teams = 22 and 1 referee, how many people do you think share the same birthday? What is the probability?
Answer 50.8%
Really?
If you take one person and check the birthday of the remaining 22 people and keep repeating this process till you find unique sets of people you will have 231 birthdays to test!.. did you know that?
In probability theory, the birthday problem or birthday paradox[1] concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367 (since there are 366 possible birthdays, including February 29). However, 99% probability is reached with just 57 people, and 50% probability with 23 people. These conclusions include the assumption that each day of the year (except February 29) is equally probable for a birthday.
Ok. Enough math!!!!
No. not enough.
No comments:
Post a Comment